Black Friday will take place on November 24. From November 17 to 19, 2023, we surveyed Canadians and Americans to learn more about their shopping habits and plans.
Download the report to learn more.
Some of the key highlights of our survey on Black Friday include…
Plans to Shop on Black Friday
- 39% of Canadians plan to make purchases on Black Friday this year, which is slightly higher than the 36% who made purchases on Black Friday last year. In comparison, 43% of Americans plan to make purchases on Black Friday this year.
- Canadians aged between 18 and 34 years (53%) and those aged 35 and 54 years (42%) are more likely to shop on Black Friday than Canadians aged 55 and older (20%).
Estimated Spending
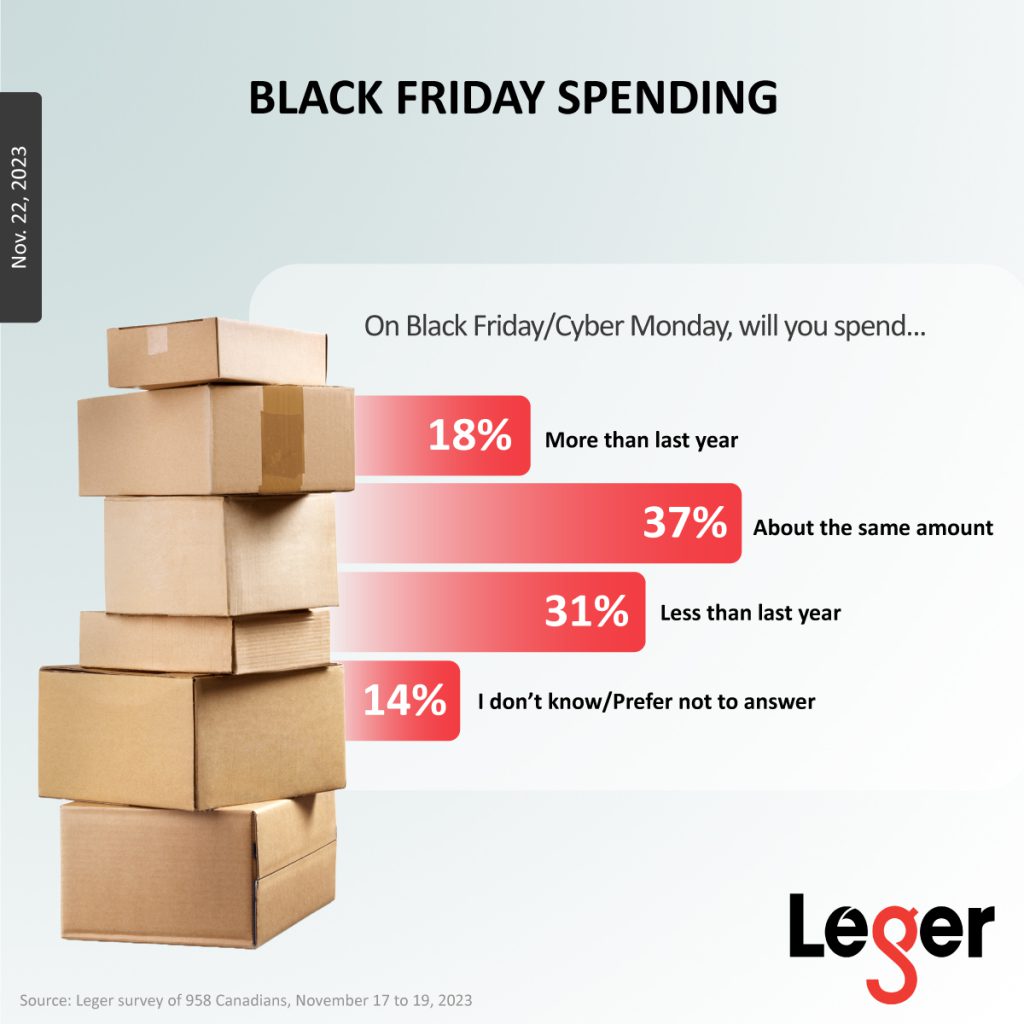
- 37% of Canadians who shop on Black Friday plan on spending the same amount as they did last year, while 31% intend to spend less, and 18% plan on buying more. In contrast, 45% of Americans plan to spend the same amount as they did last year, while 23% of them plan to spend more, and 19% plan to spend less.
- Canadians plan to spend an average of $372.60 on Black Friday this year, while Americans plan to spend significantly more, on average, $713.20.
Planned Purchase Location
- 9% of Canadians who plan to purchase items on Black Friday intend to buy primarily online, while 17% plan to buy in store. One-quarter (24%) of Canadian shoppers plan to shop both online and in store. Americans are less likely to buy in-store only (6%) and more likely to buy both in-store and online (39%).
- Both Canadians and Americans are planning on buying clothing and electronic products more than any other type of products during the Black Friday sales.
Methodology
This web survey was conducted from November 17 to 19, 2023, with 1,531 Canadians and 1,000 Americans, 18 years of age or older, randomly recruited from LEO’s online panel.
A margin of error cannot be associated with a non-probability sample in a panel survey. For comparison, a probability sample of 1,531 respondents would have a margin of error of ±2.5%, 19 times out of 20, while a probability sample of 1,000 respondents would have a margin of error of ±3.1%, 19 times out of 20.
